Nash equilibrium: intuition and examples

Nash equilibrium is a concept in game theory which is used to determine the solution of a non-cooperative game, namely a game in which the players cannot agree on a strategy together. A game is said to be in Nesh equilibrium if all the players have no incentive for changing their intial strategy considered the opponent's strategies. In other words, no player can do better by unilaterally changing his strategy. Let’s try to understand this idea and formalize it properly, applying it to some examples.

Article contents

Intuition: flow of traffic in a network

Summary

Intuition: flow of traffic in a network

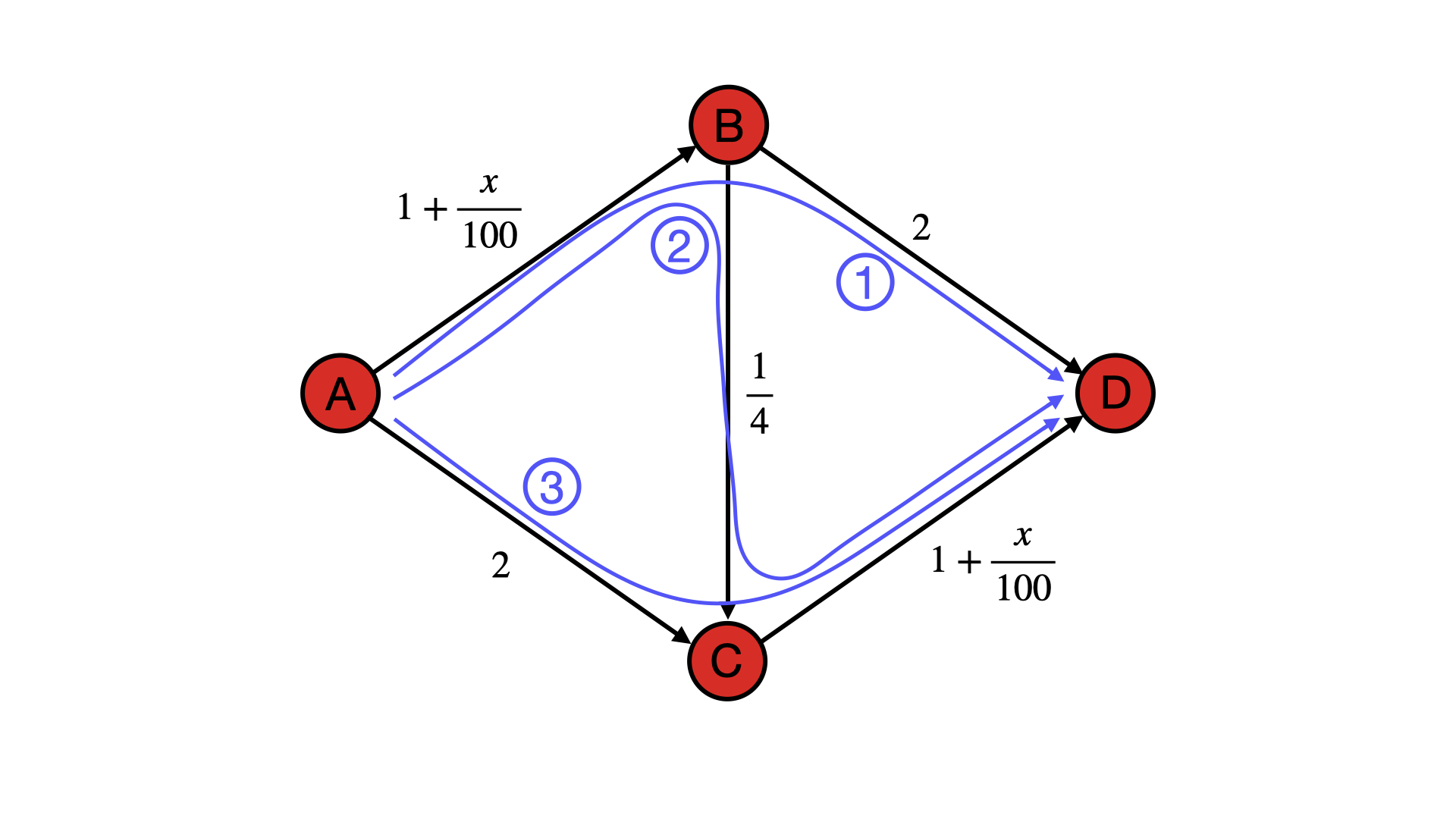
Consider the graph below representing three different routes on a road.

Let’s say there are $x$ cars traveling from A to D and the time needed to travel between two nodes is the one indicated in the corresponding edge. What is the traffic distribution we should expect from this problem?

This situation can be modeled as a non-cooperative game in that every player (driver) has to choose the shortest path but the shortest path is influenced by the choices of the other gamers (drivers), furthermore there is no joint strategy since everyone is acting in self interest. In a situation like this the natural solution to the problem is given by the Nash equilibrium, in fact that’s the situation in which everyone has no incentive to change their strategy because, by definition, they would be disadvantaged. Another way of putting it is that Nash equilibrium is the situation in which every player has the same payoff no matter the choice made and the system is somehow “balanced”. This situation is found when, eventually, every path takes exactly the same time and by deviating from this situation a driver would put the system in an unbalanced situation that would lead to longer travel time. Let’s impose this constraint in order to find the solution:

    
\begin{equation}
\big(1+\frac{x}{100}\big) + 2 = \big(1+\frac{x}{100}\big) + \frac{1}{4} + \big(1 + \frac{x}{100}\big)
\end{equation}

this equation has a solution for $x = 75$, which leads to a travel time of $\frac{15}{4}$ for each path.

Now that we have built some intuition, let's give a formal definition for the Nash equilibrium.

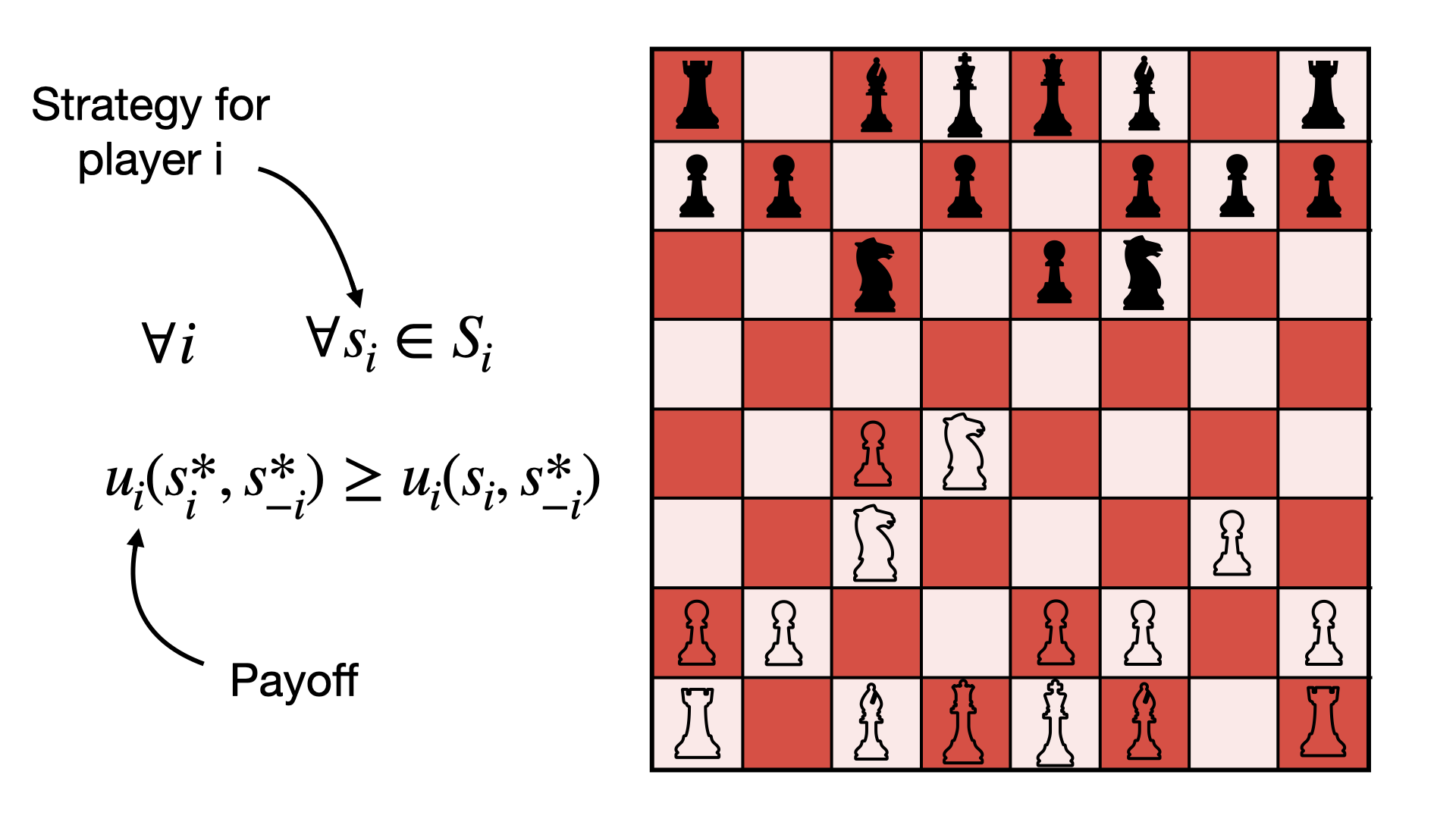
Definition

Let's define the set of possible strategies for the player $i$ with $S_i$, where $i = 1, ..., N$. Let $s^* = (s^*_i, s^*_{-i})$ be a strategy profile, where $s^*_i$ indicates the particular strategy adopted by the player $i$ and $s^*_{-i}$ the ones adopted by everyone else.
Let's define the payoff of player $i$ given its strategy as a function \begin{equation} u_i(s^*_i, s^*_{-i}) \end{equation} then the strategy profile is a Nash equilibrium if $\forall i$ \begin{equation} u_i(s^*_i, s^*_{-i}) \geq u_i(s_i, s^*_{-i}) \hspace{0.5cm} \forall s_i \in S_i \end{equation} this means, as as said, that every player has nothing to gain from changing his strategy and therefore this configuration is stable. If the inequality holds strictly, than this is said a strict Nash equilibrium

Examples:

Let’s now apply the idea of Nash equilibrium to two examples to see how it works and how to use it in practice.

The prisoner dilemma

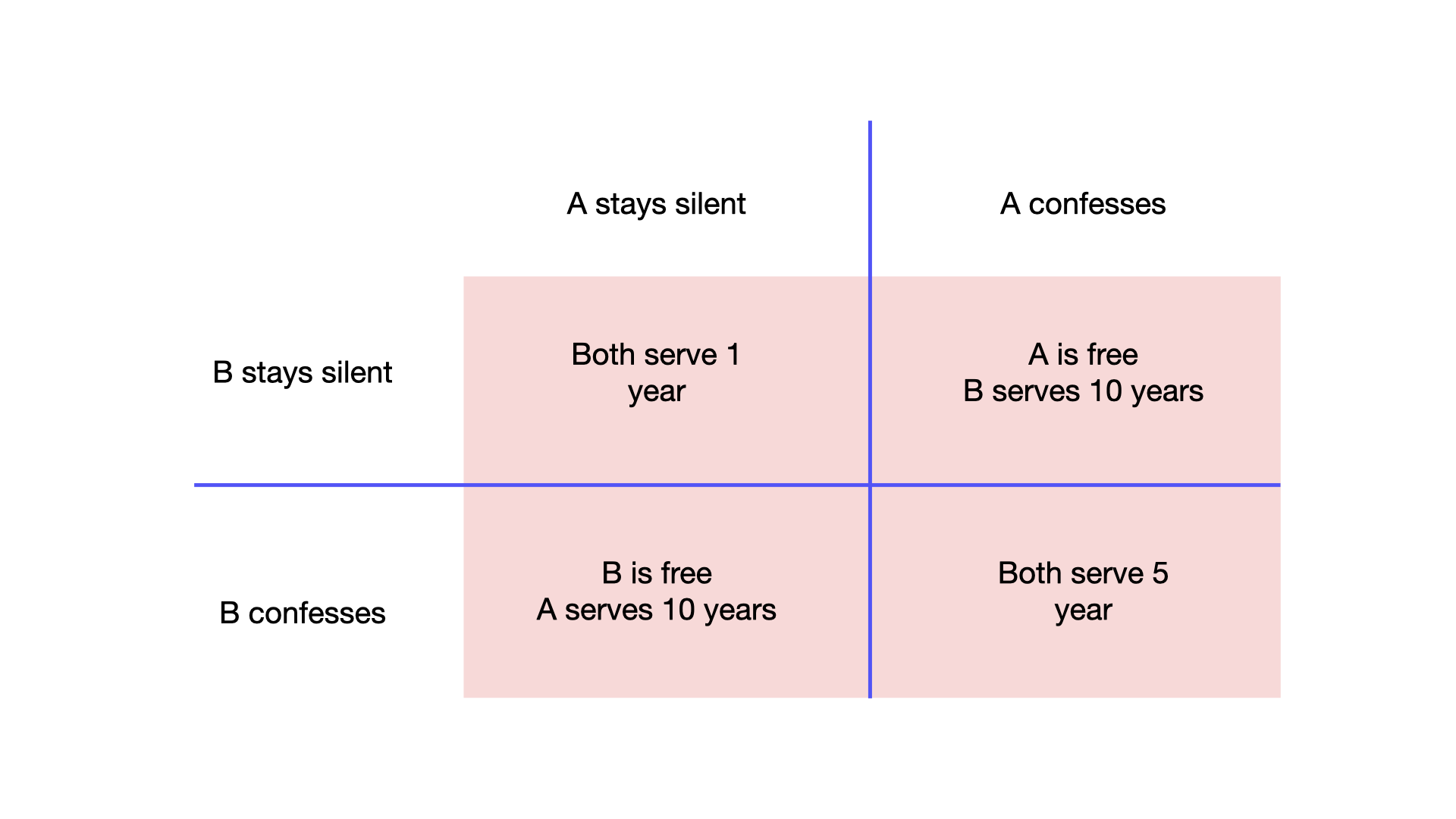
The game can be summarized like this: Player A and Player B have been arrested and placed in separated isolation cells. Both care only about their personal freedom and are offered both the following offer “You can confess or remain silent. If you confess and the other player remains silent, you are free while the other player will serve 10 years in prison. Likewise if the other player confesses and you remain silent he will be free and you will serve 10 years in prison. If you both remain silent, you will both serve 1 year in prison, while if you both confess you will serve 5 years in prison”. This game can be summarized in the following diagram

The dilemma consists in the fact that, no matter what the other player does, it is best in your self interest to confess, although the solution is not globally optimal, in that it doesn’t minimize the total number of years in prison (this would be if both stay silent) but our players are selfish. Is there a Nash equilibrium in this game? The answer is yes, let’s just follow the definition: A Nash equilibrium is a situation where every player has would be disadvantaged by changing his strategy. This is clearly true if they both confess, since staying silent would result in a personal disadvantage.

Dominant strategy:

This is also an example in which we can identify a dominant strategy, namely a strategy that is optimal regardless of what the other players are doing, in fact it is advantageous to confess, no matter what the other player does.

Let’s now look at a slightly more complicated example in that there is no dominant strategy and therefore no obvious solution to the problem. Consider the situation depicted in the graph below:

The lowest unique positive integer game

Let’s conclude by analyzing a much complex example: the lowest unique positive integer (LUPI) game.

Suppose the following game: there are three participants and they can choose an integer each. The game is won by the participant that chooses the lowest unique integer. If this condition is not satisfied (e.g. they all choose the same integer) then everyone loses. Therefore there can be either one or no winners at all. This is also known as the Lowest unique positive integer (LUPI) game.

Suppose every player is perfectly rational and egoistic, namely he acts only in his best interest. Suppose we are one of the three players: if we are not presumptuous, namely we assume everyone else is going to act as we do, what should be our optimal choice for the integer to maximize our chances of winning?

Intuitive explanation

Let's start thinking: if we all choose number 1, we all lose: this is not the best strategy. If we all choose 2, the outcome is the same, namely we all lose; the same applies to all integers of course.

This suggests that, if everyone is equally intelligent and acts rationally, the optimal solution for an individual can’t be a deterministic one. Let’s then use a probabilistic solution, namely a mixed strategy and decide to sample our choice from some distribution. Let’s say we start only with 1 and 2 and we decide flipping a coin, therefore we choose 1 with 50% and 2 with 50% probabilities. What would happen here? This is clearly better than the previous solution, in that someone wins sometimes, it might be our player. In fact, these are all possible outcomes for Player A

    
\begin{array} {r|r}\hline Player A & 1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 \\ \hline Player B & 1 & 1 & 2 & 2 & 1 & 1 & 2 & 2 \\ \hline Player C & 1 & 2 & 1 & 2 & 1 & 2 & 1 & 2 \\ \hline  & L & L & L & W & W & L & L & L   \end{array}

Let's start with a thought experiment that will hopefully lead us to the intuition behind Nash equilibrium before delving into the definition.

this means that there are two situations in which Player A actually wins, namely when the it makes a different choice while the other two make the same choice: with this strategy Player A wins 25% of the times. Same applies to Player B and Player C, while there is a 25% that everyone loses.

The fact that there is a spare 25% suggests that there is another strategy, obtained by varying the last one, which lets us recover some more winning probability.

Let’s keep going euristically: we have so far found a strategy that let’s us win in 25% of the cases (if the other players use the same strategy), what can we do next? Intuition suggests that due to the game structure, we can recover some probability by using three instead of two numbers. Let’s see what happens if we play 1, 2, and 3 with $\frac{1}{3}$ probability each. We can easily see that there are only three cases where nobody wins, namely when all the numbers are the same; this occurs $\frac{1}{9}$ of the times, which means that the remaining probability is reserved to some winner. Since they all play the same strategy it sufficies to divide the remaining probability by three, which gives a $\frac{8}{27}$ chance to win for every player. This is already higher that 25%, therefore it’s a better strategy.

Simply reasoning by induction suggests that, by simply adding numbers, every player gains some probability of winning in that they subtract probability to the events in which everyone loses. In particular, playing the first n integers with uniform probability will give a losing probability of $\frac{1}{n^2}$ and therefore everyone will have a $\frac{n^2-1}{3n^2}$ chance to win. This of course converges to $\frac{1}{3}$ as n goes to infinity.

We have made some progress, but is this the optimal game everyone can play? Clearly not, because although the probability of everyone losing goes to zero, everyone could, starting from this game, try to beat the others by giving some higher probability to higher numbers, exploiting the fact that in those cases where everyone has a different number, the lowest number wins. Remember though that every player is perfectly rational and everyone will come to the same conclusion, therefore the optimal strategy will have to involve some distribution which gives more probability to lower numbers.

Using what we have learned so far with this “mental simulation” of the game, we can come up with an idea of the solution, which will have two main characteristics: it must use a large number of integers in order to minimize the probability of every one loosing, furthermore it must give somehow more probability to lower numbers, since they give the player some advantage if we average over all other factors, therefore we expect the best strategy to look something like this.

Without going further, we can imagine that at every iteration of this “mental simulation” of the game, all three players refine their strategies to maximize their probability of winning taking into account the fact that everyone else will try doing the same. Eventually, our players will converge to a solution (provided at the end of this article) where everyone has the maximum probability of winning, and furthermore no one has any incentive in changing their game, because this would lead to an advantage for the adversaries. This configuration, where everyone is maximally satisfied and couldn't hope obtaining more, is called Nash equilibrium (Nash proved that every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium).

In other words Nash equilibrium is the formalization of a situation where every player (assumed rational and selfish) is adopting the best strategy given those of the other players, and any change would make things worse for the player.

Formal solution

Let’s now get into the math of the problem and derive the exact solution.

    


Let's call $S$ the mixed strategy all players choose to play and $s_i$ the probability of choosing number $i$ according to this stratgy. Let's call $q_j$ the probability that a player wins playing number $j$, this is given by the probability he chooses a number smaller than the other ones plus the probability the other players the same bigger number, namely

\begin{equation}
q_j = \sum_{i = 1}^{j-1} s^2_i + \big( 1 - \sum_{i = 1}^j s_i\big)^2
\end{equation}

Therefore the probability of winning using mixed strategy S is given by

\begin{equation}
Q_S = \sum_{j = 1}^{\infty} q_j s_j
\end{equation}

Now let's impose Nash equilibrium: no player has to gain an advantage for changing his strategy, and assuming every player is using the same strategy $S$. Another way of seeing is that at the Nash equilibrium every road same.... quindi.... the winning probability must be the same for every number $j$ played, namely 

\begin{equation}
q_1 = q_2 = q_3 =...
\end{equation}

if this wasn't the case and for example number 1 had a higher success chance, then a player would have an advantage in choosing a strategy assigning a higher probability to number 1. This has to be true, of course, from the point of view of every player. Imposing finally the normalization on the equilibrium distribution

\begin{equation}
\sum_i s_i = 1
\end{equation}

this is an infinite system of equations

\begin{cases}
\sum_i s_i = 1\\
\big(1 - \sum_{i = 1}^2 s_i\big)^2 = 0\\
s^2_1 + \big( 1 - \sum_{i = 1}^2 s_i\big)^2 = \sum_{i = 1}^{2} s^2_i + \big( 1 - \sum_{i = 1}^3 s_i\big)^2\\
....
\end{cases}

which has a solution (i.e. there is a Nash equilibrium) which can be computed numerically. Without going into further details, the result for the first 7 numbers is summarized in the following figure.

Lowest unique positive integer (LUPI) optimal game

It is useful to notice that this is not the optimal distribution overall, that is, in fact, the uniform distribution. Therefore in general the optimal distribution overall is not the equilibrium distribution.

Summary

Summarizing, in game theory the Nash equilibrium is the situation in which every player, which is assumed perfectly rational and selfish, has no incentive in choosing a different game than the current one, making the situation stable. In other words, in a system which is at the Nash equilibrium, for a player every choice leads to the same payoff.

The prisoner dilemma is one of the simplest examples having a Nash equilibrium (confess-confess) in that both prisoners would be personally disadvantaged staying silent. A slightly more complex example is that of a traffic network, where at the equilibrium it takes, for every player (traveler) the same amount of time to travel through every path. Finally, the lowest unique positive integer (LUPI) game is the most complicated example of a game admitting a Nash equilibrium, in that it is continuous and infinite.

Bibliography

[1] Baek, S.K. and Bernhardsson, S., 2010. Equilibrium solution to the lowest unique positive integer game. Fluctuation and Noise Letters, 9(01), pp.61-68.

[2] This answer by prof. Robert Israel